Tarski–Kuratowski algorithm

In computability theory and mathematical logic the Tarski–Kuratowski algorithm is a non-deterministic algorithm which provides an upper bound for the complexity of formulas in the arithmetical hierarchy and analytical hierarchy.

The algorithm is named after Alfred Tarski and Kazimierz Kuratowski.

Algorithm

The Tarski–Kuratowski algorithm for the arithmetical hierarchy:

Convert the formula to prenex normal form.
If the formula is quantifier-free, it is in 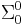$\Sigma^0_0$ and $\Pi^0_0$ .
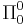Otherwise, count the number of alternations of quantifiers; call this k.
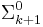If the first quantifier is ∃, the formula is in $\Sigma^0_{k%2B1}$ .
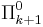If the first quantifier is ∀, the formula is in $\Pi^0_{k%2B1}$ .

References

Rogers, H. The Theory of Recursive Functions and Effective Computability, MIT Press. ISBN 0-262-68052-1; ISBN 0-07-053522-1

‹The stub template below has been proposed for renaming to . See stub types for deletion to help reach a consensus on what to do.
Feel free to edit the template, but the template must not be blanked, and this notice must not be removed, until the discussion is closed. For more information, read the guide to deletion.›